Рекурсия в Python
Оглавление
- Дорогой питоновский Дед Мороз...
- Рекурсивные функции в Python
- Сохранение состояния
- Рекурсивные структуры данных в Python
- Наивная рекурсия - это наивно
- Досадные мелочи
- Конец
- Ссылки
"Из всех идей, с которыми я знакомил детей, рекурсия выделяется как единственная идея, которая особенно способна вызвать восторженный отклик"- Сеймур Пейперт, Mindstorms
Изображение: xkcd.com
Проблемы (как в жизни, так и в информатике) часто кажутся большими и страшными. Но если мы продолжим их решать, то чаще всего сможем разбить их на более мелкие куски, достаточно тривиальные для решения. В этом и заключается суть рекурсивного мышления, и моя цель в этой статье - предоставить вам, мой дорогой читатель, концептуальные инструменты, необходимые для подхода к проблемам с этой рекурсивной точки зрения.
Вместе мы научимся работать с рекурсией в наших программах на Python, освоив такие понятия, как рекурсивные функции и рекурсивные структуры данных. Мы также поговорим о сохранении состояния во время рекурсии и избежании повторных вычислений путем кэширования результатов. Это будет очень весело. Вперед и вверх!
Дорогой питонический Дед Мороз...
Я понимаю, что, как собратья по Pythonistas, мы все здесь взрослые люди, но дети, кажется, лучше понимают красоту рекурсии. Так что давайте не на минутку перестанем быть взрослыми и поговорим о том, как можно использовать рекурсию, чтобы помочь Санта-Клаусу.
Вы когда-нибудь задумывались, как доставляются рождественские подарки? Я точно задумывался, и я верю, что у Санта-Клауса есть список домов, которые он обходит. Он приходит в один дом, отвозит подарки, съедает печенье и молоко и переходит к следующему дому в списке. Поскольку этот алгоритм доставки подарков основан на явном построении цикла, он называется итеративным алгоритмом.
Алгоритм итеративной доставки подарков, реализованный на языке Python:
houses = ["Eric's house", "Kenny's house", "Kyle's house", "Stan's house"]
def deliver_presents_iteratively():
for house in houses:
print("Delivering presents to", house)
>>> deliver_presents_iteratively()
Delivering presents to Eric's house
Delivering presents to Kenny's house
Delivering presents to Kyle's house
Delivering presents to Stan's house
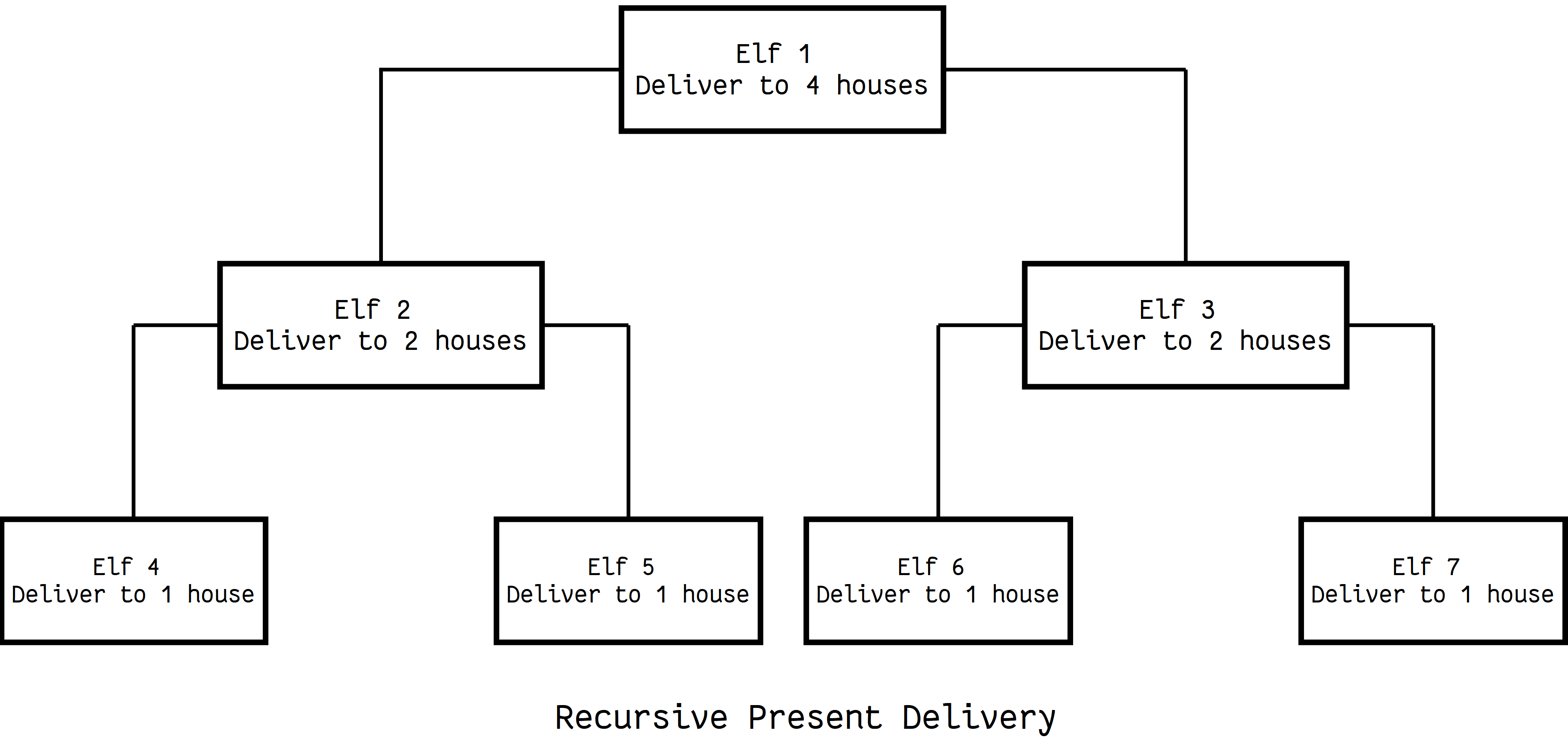
Но мне жаль Санту. В его возрасте он не должен доставлять все подарки в одиночку. Я предлагаю алгоритм, с помощью которого он может разделить работу по доставке подарков между своими эльфами:
- Назначьте эльфа и поручите ему всю работу
- Назначьте эльфам титулы и обязанности в зависимости от количества домов, за которые они отвечают:
> 1Он является управляющим и может назначить двух эльфов и разделить работу между ними= 1Он является рабочим и должен доставлять подарки в назначенный ему дом
Такова типичная структура рекурсивного алгоритма. Если текущая задача представляет собой простой случай, решите ее. Если нет, разделите ее на подпроблемы и примените к ним ту же стратегию.
Алгоритм рекурсивной доставки подарков, реализованный на языке Python:
houses = ["Eric's house", "Kenny's house", "Kyle's house", "Stan's house"]
# Each function call represents an elf doing his work
def deliver_presents_recursively(houses):
# Worker elf doing his work
if len(houses) == 1:
house = houses[0]
print("Delivering presents to", house)
# Manager elf doing his work
else:
mid = len(houses) // 2
first_half = houses[:mid]
second_half = houses[mid:]
# Divides his work among two elves
deliver_presents_recursively(first_half)
deliver_presents_recursively(second_half)
>>> deliver_presents_recursively(houses)
Delivering presents to Eric's house
Delivering presents to Kenny's house
Delivering presents to Kyle's house
Delivering presents to Stan's house
Рекурсивные функции в Python
Теперь, когда мы имеем некоторое представление о рекурсии, давайте введем формальное определение рекурсивной функции. Рекурсивная функция - это функция, определенная в терминах самой себя с помощью самореферентных выражений.
Это означает, что функция будет продолжать вызывать себя и повторять свое поведение до тех пор, пока не будет выполнено некоторое условие, позволяющее вернуть результат. Все рекурсивные функции имеют общую структуру, состоящую из двух частей: базовой и рекурсивной.
Чтобы продемонстрировать эту структуру, напишем рекурсивную функцию для вычисления n!:
-
Разложите исходную задачу на более простые экземпляры той же задачи. Это рекурсивный случай:
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1 n! = n x (n−1)! -
По мере разбиения большой проблемы на последовательно менее сложные подпроблемы, эти подпроблемы должны в конце концов стать настолько простыми, чтобы их можно было решить без дальнейшего разбиения. Это и есть базовый случай:
n! = n x (n−1)! n! = n x (n−1) x (n−2)! n! = n x (n−1) x (n−2) x (n−3)! ⋅ ⋅ n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1!
Здесь 1! - наш базовый случай, и он равен 1.
Рекурсивная функция для вычисления n! реализована на Python:
def factorial_recursive(n):
# Base case: 1! = 1
if n == 1:
return 1
# Recursive case: n! = n * (n-1)!
else:
return n * factorial_recursive(n-1)
>>> factorial_recursive(5)
120
За кулисами каждый рекурсивный вызов добавляет стековый кадр (содержащий его контекст выполнения) в стек вызовов, пока мы не достигнем базового случая. Затем стек начинает разворачиваться по мере того, как каждый вызов возвращает свои результаты:
Поддерживая состояние
При работе с рекурсивными функциями следует помнить, что каждый рекурсивный вызов имеет свой собственный контекст выполнения, поэтому для сохранения состояния во время рекурсии необходимо либо:
- Пропускайте состояние через каждый рекурсивный вызов так, чтобы текущее состояние было частью контекста выполнения текущего вызова
- Храните состояние в глобальной области видимости
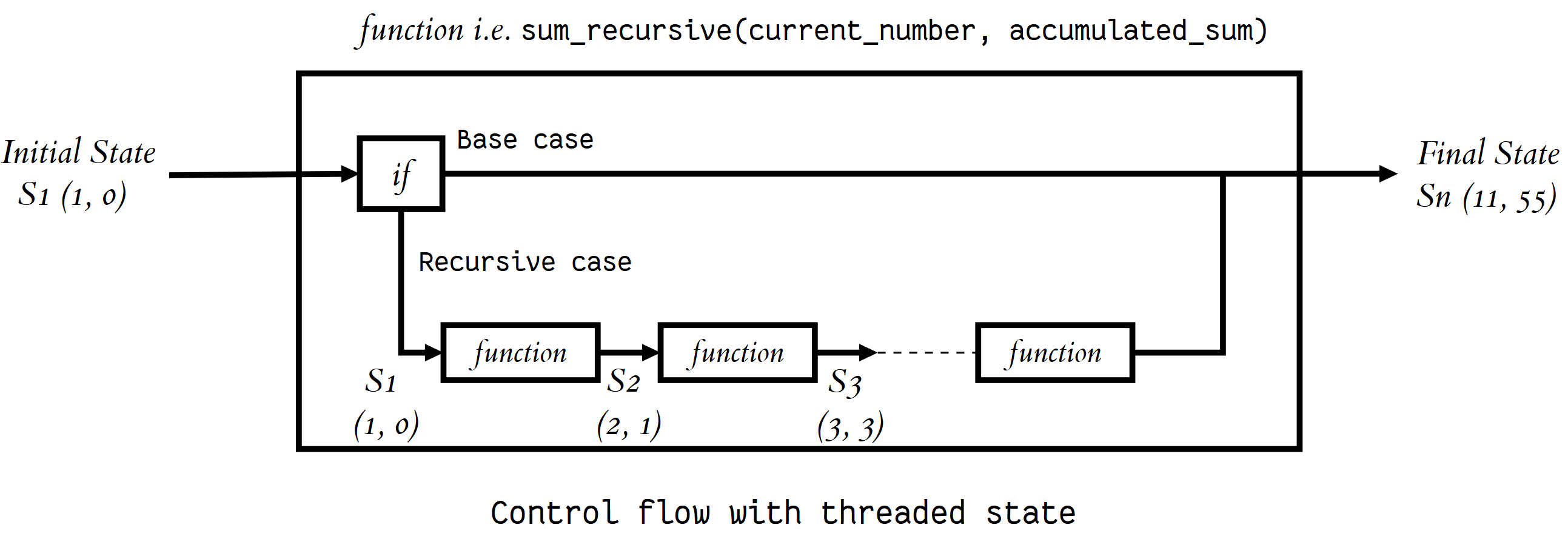
Демонстрация должна прояснить ситуацию. Давайте вычислим 1 + 2 + 3 ⋅⋅⋅⋅ + 10 с помощью рекурсии. Состояние, которое мы должны поддерживать, (текущее число, которое мы добавляем, накопленная сумма до настоящего момента).
Вот как вы это сделаете, пропуская через каждый рекурсивный вызов (т.е. передавая обновленное текущее состояние в каждый рекурсивный вызов в качестве аргументов):
def sum_recursive(current_number, accumulated_sum):
# Base case
# Return the final state
if current_number == 11:
return accumulated_sum
# Recursive case
# Thread the state through the recursive call
else:
return sum_recursive(current_number + 1, accumulated_sum + current_number)
# Pass the initial state
>>> sum_recursive(1, 0)
55
Вот как вы поддерживаете состояние, сохраняя его в глобальном scope:
# Global mutable state
current_number = 1
accumulated_sum = 0
def sum_recursive():
global current_number
global accumulated_sum
# Base case
if current_number == 11:
return accumulated_sum
# Recursive case
else:
accumulated_sum = accumulated_sum + current_number
current_number = current_number + 1
return sum_recursive()
>>> sum_recursive()
55
Я предпочитаю передавать состояние через каждый рекурсивный вызов, потому что считаю глобальные мутабельные состояния злом, но об этом мы поговорим позже.
Рекурсивные структуры данных в Python
Структура данных является рекурсивной, если она может быть определена в терминах меньшей версии самой себя. Примером рекурсивной структуры данных является список. Позвольте мне продемонстрировать это. Предположим, что в вашем распоряжении есть только пустой список, и единственная операция, которую вы можете выполнить над ним, такова:
# Return a new list that is the result of
# adding element to the head (i.e. front) of input_list
def attach_head(element, input_list):
return [element] + input_list
Используя пустой список и операцию attach_head, можно сгенерировать любой список. Например, сгенерируем [1, 46, -31, "hello"]:
attach_head(1, # Will return [1, 46, -31, "hello"]
attach_head(46, # Will return [46, -31, "hello"]
attach_head(-31, # Will return [-31, "hello"]
attach_head("hello", [])))) # Will return ["hello"]
[1, 46, -31, 'hello']
-
Начиная с пустого списка, вы можете сгенерировать любой список, рекурсивно применяя функцию
attach_head, и таким образом структура данных списка может быть определена рекурсивно как:+---- attach_head(element, smaller list) list = + +---- empty list -
Рекурсию также можно рассматривать как самореферентную композицию функций. Мы применяем функцию к аргументу, затем передаем результат в качестве аргумента для второго применения той же функции и так далее. Многократная композиция
attach_headс самим собой - это то же самое, чтоattach_headмногократно вызывать самого себя.
List - не единственная рекурсивная структура данных. Другие примеры включают set, дерево, dictionary и т. д.
Рекурсивные структуры данных и рекурсивные функции сочетаются как хлеб с маслом. Структура рекурсивной функции часто может быть смоделирована на основе определения рекурсивной структуры данных, которую она принимает на вход. Позвольте мне продемонстрировать это на примере рекурсивного вычисления суммы всех элементов списка:
def list_sum_recursive(input_list):
# Base case
if input_list == []:
return 0
# Recursive case
# Decompose the original problem into simpler instances of the same problem
# by making use of the fact that the input is a recursive data structure
# and can be defined in terms of a smaller version of itself
else:
head = input_list[0]
smaller_list = input_list[1:]
return head + list_sum_recursive(smaller_list)
>>> list_sum_recursive([1, 2, 3])
6
Наивная рекурсия является наивной
Числа Фибоначчи были первоначально определены итальянским математиком Фибоначчи в тринадцатом веке для моделирования роста популяции кроликов. Фибоначчи предположил, что количество пар кроликов, рожденных в определенный год, равно количеству пар кроликов, рожденных в каждый из двух предыдущих лет, начиная с одной пары кроликов в первый год.
Для подсчета количества кроликов, родившихся в n-ом году, он определил рекуррентное соотношение:
Fn = Fn-1 + Fn-2
Базовыми случаями являются:
F0 = 0 and F1 = 1
Давайте напишем рекурсивную функцию для вычисления n-го числа Фибоначчи:
def fibonacci_recursive(n):
print("Calculating F", "(", n, ")", sep="", end=", ")
# Base case
if n == 0:
return 0
elif n == 1:
return 1
# Recursive case
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
>>> fibonacci_recursive(5)
Calculating F(5), Calculating F(4), Calculating F(3), Calculating F(2), Calculating F(1),
Calculating F(0), Calculating F(1), Calculating F(2), Calculating F(1), Calculating F(0),
Calculating F(3), Calculating F(2), Calculating F(1), Calculating F(0), Calculating F(1),
5
Наивное следование рекурсивному определению n-го числа Фибоначчи оказалось довольно неэффективным. Как видно из приведенного выше результата, мы без необходимости пересчитываем значения. Попробуем улучшить fibonacci_recursive, кэшируя результаты каждого вычисления Фибоначчи Fk:
from functools import lru_cache
@lru_cache(maxsize=None)
def fibonacci_recursive(n):
print("Calculating F", "(", n, ")", sep="", end=", ")
# Base case
if n == 0:
return 0
elif n == 1:
return 1
# Recursive case
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
>>> fibonacci_recursive(5)
Calculating F(5), Calculating F(4), Calculating F(3), Calculating F(2), Calculating F(1), Calculating F(0),
5
lru_cache - это декоратор, который кэширует результаты. Таким образом, мы избегаем повторных вычислений, явно проверяя значение перед тем, как попытаться его вычислить. Следует помнить, что поскольку функция lru_cache использует словарь для кэширования результатов, позиционные и ключевые аргументы (которые служат ключами в этом словаре) функции должны быть хэшируемыми.
Досадные мелочи
В Python нет поддержки устранения хвостовых вызовов. В результате вы можете вызвать переполнение стека, если в итоге используете больше стековых кадров, чем глубина стека вызовов по умолчанию:
>>> import sys
>>> sys.getrecursionlimit()
1000
Помните об этом ограничении, если у вас есть программа, требующая глубокой рекурсии.
Кроме того, мутабельные структуры данных Python не поддерживают структурное разделение, поэтому обращение с ними как с неизменяемыми структурами данных негативно скажется на эффективности использования пространства и GC (сборки мусора), поскольку в итоге вы будете без необходимости копировать множество мутабельных объектов. Например, я использовал этот паттерн для декомпозиции списков и рекурсии по ним:
>>> input_list = [1, 2, 3]
>>> head = input_list[0]
>>> tail = input_list[1:]
>>> print("head --", head)
head -- 1
>>> print("tail --", tail)
tail -- [2, 3]
Я сделал это, чтобы упростить ситуацию для наглядности. Имейте в виду, что хвост создается путем копирования. Рекурсивное выполнение этого действия над большими списками может негативно сказаться на пространстве и эффективности GC.
Конец
Однажды на собеседовании меня попросили объяснить, что такое рекурсия. Я взял лист бумаги и написал Please turn over на обеих сторонах. Интервьюер не понял шутки, но теперь, когда вы прочитали эту статью, надеюсь, понял 🙂 Happy Pythoning!
Сыылки
- Мыслить рекурсивно
- Маленький интриган
- Концепции, методы и модели компьютерного программирования
- Руководство по проектированию алгоритмов
- Программирование на языке Хаскель с первых принципов