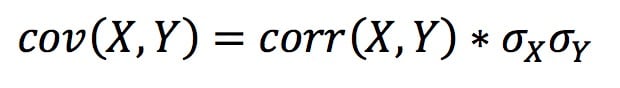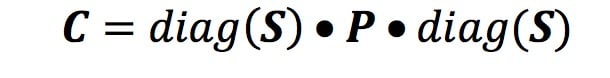Генерация случайных данных в Python

Оглавление

Насколько случайным является случайность? Это странный вопрос, но он имеет первостепенное значение в случаях, когда речь идет об информационной безопасности. Всякий раз, когда вы генерируете случайные данные, строки или числа в Python, неплохо иметь хотя бы приблизительное представление о том, как эти данные были сгенерированы.

Здесь вы рассмотрите несколько различных вариантов генерации случайных данных в Python, а затем проведете сравнение каждого из них с точки зрения уровня безопасности, универсальности, назначения и скорости.

Обещаю, что этот учебник не будет уроком математики или криптографии, для чтения лекций по которым у меня нет достаточной подготовки. Вы получите ровно столько математики, сколько нужно, и не больше.

Насколько случайна случайность?

Во-первых, необходимо поместить на видном месте отказ от ответственности. Большинство случайных данных, генерируемых с помощью Python, не являются полностью случайными в научном смысле этого слова. Скорее, они псевдослучайны: генерируются с помощью генератора псевдослучайных чисел (ГПСЧ), который по сути является любым алгоритмом для генерации кажущихся случайными, но все же воспроизводимых данных.

"Истинные" случайные числа могут быть сгенерированы, как вы уже догадались, генератором истинных случайных чисел (TRNG). Один из примеров - многократно поднимать кубик с пола, подбрасывать его в воздух и позволять ему приземляться так, как ему вздумается.

Предполагая, что ваш бросок беспристрастен, вы не имеете ни малейшего представления о том, какое число выпадет на кубике. Бросок кубика - это грубая форма использования аппаратуры для генерации числа, которое не является детерминированным. (Или вы можете попросить dice-o-matic сделать это за вас). TRNG выходят за рамки этой статьи, но все же заслуживают упоминания для сравнения.

PRNG, обычно выполняемые программно, а не аппаратно, работают несколько иначе. Вот краткое описание:

Они начинают со случайного числа, известного как затравка, а затем используют алгоритм для генерации псевдослучайной последовательности битов на его основе. (Источник)

Вероятно, вам когда-то говорили: "Читайте документацию!". Что ж, эти люди не ошибаются. Вот особенно примечательный фрагмент из документации модуля random, который вы не должны пропустить:

Предупреждение: Псевдослучайные генераторы этого модуля не должны использоваться в целях безопасности. (Источник)

Вы наверняка встречали в Python выражения random.seed(999), random.seed(1234) и им подобные. Этот вызов функции засевает базовый генератор случайных чисел, используемый модулем Python random. Именно он делает последующие вызовы генерации случайных чисел детерминированными: на входе A всегда получается выход B. Это благословение может стать и проклятием, если использовать его со злым умыслом.

Возможно, термины "случайный" и "детерминированный" кажутся такими, что не могут существовать рядом друг с другом. Чтобы прояснить это, вот крайне урезанная версия random(), которая итеративно создает "случайное" число с помощью x = (x * 3) % 19. x изначально определяется как начальное значение, а затем превращается в детерминированную последовательность чисел, основанную на этом значении:

class NotSoRandom(object):
    def seed(self, a=3):
        """Seed the world's most mysterious random number generator."""
        self.seedval = a
    def random(self):
        """Look, random numbers!"""
        self.seedval = (self.seedval * 3) % 19
        return self.seedval

_inst = NotSoRandom()
seed = _inst.seed
random = _inst.random

Не воспринимайте этот пример слишком буквально, так как он предназначен в основном для иллюстрации концепции. Если вы используете начальное значение 1234, то последующая последовательность вызовов random() должна быть всегда одинаковой:

>>> seed(1234)
>>> [random() for _ in range(10)]
[16, 10, 11, 14, 4, 12, 17, 13, 1, 3]

>>> seed(1234)
>>> [random() for _ in range(10)]
[16, 10, 11, 14, 4, 12, 17, 13, 1, 3]

Вскоре вы увидите более серьезную иллюстрацию к этому.

Что такое "криптографическая безопасность?"

Если вам еще не надоели аббревиатуры "ГПСЧ", давайте добавим еще одну: CSPRNG, или криптографически защищенный ГПСЧ. ГПСЧ подходят для генерации конфиденциальных данных, таких как пароли, аутентификаторы и токены. Учитывая случайную строку, злоумышленник не сможет определить, какая строка идет до или после этой строки в последовательности случайных строк.

Еще один термин, который вы можете встретить, это энтропия. В двух словах, это обозначает количество вносимой или желаемой случайности. Например, один из модулей Python , о котором вы будете рассказывать здесь, определяет DEFAULT_ENTROPY = 32, количество байт, возвращаемых по умолчанию. Разработчики считают, что это "достаточное" количество байтов, чтобы обеспечить достаточный уровень шума.

Примечание: В этом учебнике я предполагаю, что байт обозначает 8 бит, как это принято с 1960-х годов, а не какую-то другую единицу хранения данных. Вы можете называть это октетом, если вам так больше нравится.

Ключевым моментом в работе CSPRNG является то, что они все еще остаются псевдослучайными. Они сконструированы таким образом, что внутренне детерминированы, но в них добавлена еще одна переменная или есть какое-то свойство, которое делает их достаточно "случайными", чтобы запретить обратный ход в любой функции, принуждающей к детерминизму.

Что вы здесь узнаете

С практической точки зрения это означает, что вам следует использовать обычные ГПСЧ для статистического моделирования, симуляции и для воспроизведения случайных данных. Они также значительно быстрее, чем CSPRNG, как вы увидите далее. Используйте CSPRNG для обеспечения безопасности и криптографических приложений, где чувствительность данных является обязательной.

В дополнение к расширению описанных выше примеров использования, в этом уроке вы изучите инструменты Python для использования как ГПСЧ, так и ГПСЧ:

  • Варианты ГПСЧ включают модуль random из стандартной библиотеки Python и его аналог NumPy, основанный на массивах, numpy.random.
  • Модули Python os, secrets и uuid содержат функции для генерации криптографически защищенных объектов.

Вы затронете все вышеперечисленное и завершите сравнение на высоком уровне.

ГПСЧ в Python

Модуль random

Пожалуй, самым известным инструментом для генерации случайных данных в Python является его модуль random, который использует в качестве основного генератора алгоритм Mersenne Twister PRNG.

Ранее вы вкратце коснулись random.seed(), и сейчас самое время посмотреть, как это работает. Сначала давайте построим случайные данные без посева. Функция random.random() возвращает случайное число float в интервале [0.0, 1.0). Результат всегда будет меньше правой конечной точки (1,0). Это также известно как полуоткрытый интервал:

>>> # Don't call `random.seed()` yet
>>> import random
>>> random.random()
0.35553263284394376
>>> random.random()
0.6101992345575074

Если вы запустите этот код самостоятельно, я готов поспорить на свои сбережения, что числа, возвращаемые на вашей машине, будут другими. По умолчанию, когда вы не засеваете генератор, используется текущее системное время или "источник случайности" из вашей ОС, если таковой имеется.

С помощью random.seed() можно сделать результаты воспроизводимыми, и цепочка вызовов после random.seed() будет давать один и тот же след данных:

>>> random.seed(444)
>>> random.random()
0.3088946587429545
>>> random.random()
0.01323751590501987

>>> random.seed(444)  # Re-seed
>>> random.random()
0.3088946587429545
>>> random.random()
0.01323751590501987

Обратите внимание на повторение "случайных" чисел. Последовательность случайных чисел становится детерминированной, или полностью определяемой начальным значением, 444.

Давайте рассмотрим некоторые основные функции random. Выше вы сгенерировали случайное число float. В Python вы можете сгенерировать случайное целое число между двумя конечными точками с помощью функции random.randint(). Она охватывает весь интервал [x, y] и может включать обе конечные точки:

>>> random.randint(0, 10)
7
>>> random.randint(500, 50000)
18601

С помощью random.randrange() можно исключить правую часть интервала, то есть сгенерированное число всегда лежит в пределах [x, y) и всегда будет меньше правой конечной точки:

>>> random.randrange(1, 10)
5

Если вам нужно сгенерировать случайные числа, лежащие в определенном интервале [x, y], вы можете использовать random.uniform(), который берет значения из непрерывного равномерного распределения :

>>> random.uniform(20, 30)
27.42639687016509
>>> random.uniform(30, 40)
36.33865802745107

Чтобы выбрать случайный элемент из непустой последовательности (например, списка или кортежа ), вы можете использовать random.choice(). Существует также random.choices() для выбора нескольких элементов из последовательности с заменой (возможны дубликаты):

>>> items = ['one', 'two', 'three', 'four', 'five']
>>> random.choice(items)
'four'

>>> random.choices(items, k=2)
['three', 'three']
>>> random.choices(items, k=3)
['three', 'five', 'four']

Чтобы имитировать выборку без замены, используйте random.sample():

>>> random.sample(items, 4)
['one', 'five', 'four', 'three']

Вы можете рандомизировать последовательность на месте, используя random.shuffle(). Это изменит объект последовательности и рандомизирует порядок элементов:

>>> random.shuffle(items)
>>> items
['four', 'three', 'two', 'one', 'five']

Если вы не хотите мутировать исходный список, вам нужно сначала создать его копию, а затем перетасовать ее. Вы можете создавать копии списков Python с помощью модуля copy, или просто x[:] или x.copy(), где x - список.

Прежде чем перейти к генерации случайных данных с помощью NumPy, давайте рассмотрим еще одно немного сложное приложение: генерацию последовательности уникальных случайных строк одинаковой длины.

Сначала стоит подумать о дизайне функции. Вам нужно выбрать из "пула" символов, таких как буквы, цифры и/или знаки препинания, объединить их в одну строку, а затем проверить, что эта строка еще не была сгенерирована. Для такого типа тестирования членства хорошо подходит Python set:

import string

def unique_strings(k: int, ntokens: int,
               pool: str=string.ascii_letters) -> set:
    """Generate a set of unique string tokens.

    k: Length of each token
    ntokens: Number of tokens
    pool: Iterable of characters to choose from

    For a highly optimized version:
    https://stackoverflow.com/a/48421303/7954504
    """

    seen = set()

    # An optimization for tightly-bound loops:
    # Bind these methods outside of a loop
    join = ''.join
    add = seen.add

    while len(seen) < ntokens:
        token = join(random.choices(pool, k=k))
        add(token)
    return seen

''.join() объединяет буквы из random.choices() в один Python str длины k. Эта лексема добавляется к множеству, которое не может содержать дубликатов, и цикл while выполняется до тех пор, пока множество не наберет указанное вами количество элементов.

Ресурс: Модуль Python string содержит ряд полезных констант: ascii_lowercase, ascii_uppercase, string.punctuation, ascii_whitespace и ряд других.

Давайте попробуем использовать эту функцию:

>>> unique_strings(k=4, ntokens=5)
{'AsMk', 'Cvmi', 'GIxv', 'HGsZ', 'eurU'}

>>> unique_strings(5, 4, string.printable)
{"'O*1!", '9Ien%', 'W=m7<', 'mUD|z'}

Для получения более точной версии этой функции в этом ответе Stack Overflow используются функции-генераторы, привязка имен и некоторые другие продвинутые трюки для создания более быстрой и криптографически безопасной версии unique_strings() выше.

ГПСЧ для массивов: numpy.random

Вы могли заметить, что большинство функций из random возвращают скалярное значение (один int, float или другой объект). Если бы вы хотели сгенерировать последовательность случайных чисел, то одним из способов достижения этой цели было бы использование Python понимания списка:

>>> [random.random() for _ in range(5)]
[0.021655420657909374,
 0.4031628347066195,
 0.6609991871223335,
 0.5854998250783767,
 0.42886606317322706]

Но есть и другой вариант, специально предназначенный для этого. Собственный пакет NumPy numpy.random можно рассматривать как подобие стандартной библиотеки random, но для массивов NumPy. (В него также добавлена возможность брать данные из гораздо большего числа статистических распределений)

Обратите внимание, что numpy.random использует свой собственный ГПСЧ, отдельный от старого доброго random. Вы не сможете получить детерминированно случайные массивы NumPy с помощью вызова собственного random.seed():

>>> import numpy as np
>>> np.random.seed(444)
>>> np.set_printoptions(precision=2)  # Output decimal fmt.

Без лишних слов, вот несколько примеров, чтобы разжечь ваш аппетит:

>>> # Return samples from the standard normal distribution
>>> np.random.randn(5)
array([ 0.36,  0.38,  1.38,  1.18, -0.94])

>>> np.random.randn(3, 4)
array([[-1.14, -0.54, -0.55,  0.21],
       [ 0.21,  1.27, -0.81, -3.3 ],
       [-0.81, -0.36, -0.88,  0.15]])

>>> # `p` is the probability of choosing each element
>>> np.random.choice([0, 1], p=[0.6, 0.4], size=(5, 4))
array([[0, 0, 1, 0],
       [0, 1, 1, 1],
       [1, 1, 1, 0],
       [0, 0, 0, 1],
       [0, 1, 0, 1]])

В синтаксисе для randn(d0, d1, ..., dn) параметры d0, d1, ..., dn являются необязательными и указывают на форму конечного объекта. Здесь np.random.randn(3, 4) создает двумерный массив с 3 строками и 4 столбцами. Данные будут i.i.d., что означает, что каждая точка данных рисуется независимо от других.

Примечание: Если вы хотите создать нормально распределенные случайные числа, то вам повезло! How to Get Normally Distributed Random Numbers With NumPy может указать вам путь.

Другая распространенная операция - создание последовательности случайных булевых значений , True или False. Один из способов сделать это - np.random.choice([True, False]). Однако на самом деле примерно в 4 раза быстрее выбрать одно из (0, 1) и затем перегнать эти целые числа в соответствующие им булевы значения:

>>> # NumPy's `randint` is [inclusive, exclusive), unlike `random.randint()`
>>> np.random.randint(0, 2, size=25, dtype=np.uint8).view(bool)
array([ True, False,  True,  True, False,  True, False, False, False,
       False, False,  True,  True, False, False, False,  True, False,
        True, False,  True,  True,  True, False,  True])

А как насчет генерации коррелированных данных? Допустим, вы хотите смоделировать два коррелированных временных ряда. Один из способов сделать это - использовать функцию NumPy multivariate_normal(), которая учитывает ковариационную матрицу. Другими словами, чтобы получить данные от одной нормально распределенной случайной величины, необходимо указать ее среднее значение и дисперсию (или стандартное отклонение).

Чтобы сделать выборку из многомерного нормального распределения, вы задаете средние значения и ковариационную матрицу, и в итоге получаете несколько коррелированных рядов данных, каждый из которых распределен приблизительно нормально.

Однако более привычной и интуитивно понятной для большинства мерой является не ковариация, а корреляция. Это ковариация, нормированная на произведение стандартных отклонений, и поэтому ковариацию можно также определить в терминах корреляции и стандартного отклонения:

Covariance in Scalar Form

Итак, можно ли получить случайные выборки из многомерного нормального распределения, задав корреляционную матрицу и стандартные отклонения? Да, но сначала нужно привести к матричному виду . Здесь S - вектор стандартных отклонений, P - их корреляционная матрица, а C - результирующая (квадратная) ковариационная матрица:

Covariance in Matrix Form

Это можно выразить в NumPy следующим образом:

def corr2cov(p: np.ndarray, s: np.ndarray) -> np.ndarray:
    """Covariance matrix from correlation & standard deviations"""
    d = np.diag(s)
    return d @ p @ d

Теперь вы можете сгенерировать два временных ряда, которые коррелируют, но остаются случайными:

>>> # Start with a correlation matrix and standard deviations.
>>> # -0.40 is the correlation between A and B, and the correlation
>>> # of a variable with itself is 1.0.
>>> corr = np.array([[1., -0.40],
...                  [-0.40, 1.]])

>>> # Standard deviations/means of A and B, respectively
>>> stdev = np.array([6., 1.])
>>> mean = np.array([2., 0.5])
>>> cov = corr2cov(corr, stdev)

>>> # `size` is the length of time series for 2d data
>>> # (500 months, days, and so on).
>>> data = np.random.multivariate_normal(mean=mean, cov=cov, size=500)
>>> data[:10]
array([[ 0.58,  1.87],
       [-7.31,  0.74],
       [-6.24,  0.33],
       [-0.77,  1.19],
       [ 1.71,  0.7 ],
       [-3.33,  1.57],
       [-1.13,  1.23],
       [-6.58,  1.81],
       [-0.82, -0.34],
       [-2.32,  1.1 ]])
>>> data.shape
(500, 2)

Вы можете представить data как 500 пар обратно коррелированных точек данных. Вот проверка на вменяемость, которую можно вернуть в исходные данные, аппроксимирующие corr, stdev и mean сверху:

>>> np.corrcoef(data, rowvar=False)
array([[ 1.  , -0.39],
       [-0.39,  1.  ]])

>>> data.std(axis=0)
array([5.96, 1.01])

>>> data.mean(axis=0)
array([2.13, 0.49])

Прежде чем мы перейдем к рассмотрению CSPRNG, будет полезно кратко описать некоторые random функции и их numpy.random аналоги:

Python random Module NumPy Counterpart Use
random() rand() Random float in [0.0, 1.0)
randint(a, b) random_integers() Random integer in [a, b]
randrange(a, b[, step]) randint() Random integer in [a, b)
uniform(a, b) uniform() Random float in [a, b]
choice(seq) choice() Random element from seq
choices(seq, k=1) choice() Random k elements from seq with replacement
sample(population, k) choice() with replace=False Random k elements from seq without replacement
shuffle(x[, random]) shuffle() Shuffle the sequence x in place
normalvariate(mu, sigma) or gauss(mu, sigma) normal() Sample from a normal distribution with mean mu and standard deviation sigma

Примечание: NumPy специализируется на построении и работе с большими многомерными массивами. Если вам нужно только одно значение, достаточно random, и, вероятно, это будет быстрее. Для небольших последовательностей random может быть даже быстрее, потому что NumPy все же имеет некоторые накладные расходы.

Теперь, когда вы рассмотрели два основных варианта ГПСЧ, давайте перейдем к нескольким более безопасным адаптациям.

CSPRNG в Python

os.urandom(): About as Random as It Gets

Функцияn os.urandom() используется как secrets, так и uuid (обе эти функции вы увидите здесь через некоторое время). Не вдаваясь в излишние подробности, os.urandom() генерирует зависящие от операционной системы случайные байты, которые можно смело назвать криптографически безопасными:

  • В операционных системах Unix он считывает случайные байты из специального файла /dev/urandom, которые, в свою очередь, "позволяют получить доступ к шуму окружающей среды, собранному из драйверов устройств и других источников". (Спасибо, Wikipedia). Это беспорядочная информация, характерная для вашего оборудования и состояния системы в данный момент времени, но в то же время достаточно случайная.

  • В Windows используется функция C++ CryptGenRandom(). Эта функция все еще технически является псевдослучайной, но она работает путем генерации начального значения из таких переменных, как идентификатор процесса, состояние памяти и так далее.

При os.urandom() отсутствует понятие ручного посева. Хотя технически эта функция все еще остается псевдослучайной, она лучше согласуется с тем, как мы представляем себе случайность. Единственным аргументом является количество байт, которое нужно вернуть:

>>> os.urandom(3)
b'\xa2\xe8\x02'

>>> x = os.urandom(6)
>>> x
b'\xce\x11\xe7"!\x84'

>>> type(x), len(x)
(bytes, 6)

Прежде чем мы продолжим, самое время провести мини-урок по кодировке символов. У многих людей, в том числе и у меня, возникает своего рода аллергическая реакция при виде объектов bytes и длинной строки символов \x. Однако полезно знать, как такие последовательности, как x выше, в конечном итоге превращаются в строки или числа.

os.urandom() возвращает последовательность одиночных байтов:

>>> x
b'\xce\x11\xe7"!\x84'

Но как это в итоге превращается в Python str или последовательность чисел?

Для начала вспомним одну из фундаментальных концепций вычислений: байт состоит из 8 битов. Бит можно представить как одну цифру, которая равна либо 0, либо 1. Байт фактически выбирает между 0 и 1 восемь раз, поэтому и 01101100, и 11110000 могут представлять собой байты. Попробуйте использовать в интерпретаторе Python f-строки, введенные в Python 3.6:

>>> binary = [f'{i:0>8b}' for i in range(256)]
>>> binary[:16]
['00000000',
 '00000001',
 '00000010',
 '00000011',
 '00000100',
 '00000101',
 '00000110',
 '00000111',
 '00001000',
 '00001001',
 '00001010',
 '00001011',
 '00001100',
 '00001101',
 '00001110',
 '00001111']

Это эквивалентно [bin(i) for i in range(256)], с некоторым специальным форматированием. bin() преобразует целое число в его двоичное представление в виде строки.

Что же остается нам? Использование range(256) выше не является случайным выбором. (Учитывая, что нам разрешено 8 бит, каждый из которых имеет 2 варианта, существует 2 ** 8 == 256 возможных "комбинаций" байтов.

Это означает, что каждый байт соответствует целому числу от 0 до 255. Другими словами, для выражения целого числа 256 нам потребуется более 8 бит. Вы можете убедиться в этом, проверив, что len(f'{256:0>8b}') теперь равно 9, а не 8.

Хорошо, теперь давайте вернемся к типу данных bytes, который вы видели выше, построив последовательность байтов, соответствующих целым числам от 0 до 255:

>>> bites = bytes(range(256))

Если вы вызовете list(bites), вы вернетесь к списку Python, который начинается от 0 до 255. Но если вы просто напечатаете bites, то получите уродливую последовательность, замусоренную обратными косыми чертами:

>>> bites
b'\x00\x01\x02\x03\x04\x05\x06\x07\x08\t\n\x0b\x0c\r\x0e\x0f\x10\x11\x12\x13\x14\x15'
 '\x16\x17\x18\x19\x1a\x1b\x1c\x1d\x1e\x1f !"#$%&\'()*+,-./0123456789:;<=>?@ABCDEFGHIJK'
 'LMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~\x7f\x80\x81\x82\x83\x84\x85\x86'
 '\x87\x88\x89\x8a\x8b\x8c\x8d\x8e\x8f\x90\x91\x92\x93\x94\x95\x96\x97\x98\x99\x9a\x9b'

 # ...

Эти обратные косые черты являются управляющими последовательностями, а \xhh представляет собой символ с шестнадцатеричным значением hh. Некоторые из элементов bites отображаются буквально (печатаемые символы, такие как буквы, цифры и знаки препинания). Большинство выражается с помощью эскейпов. \x08 представляет собой пробел на клавиатуре, а \x13 - возврат каретки (часть новой строки, в системах Windows).

Если вам нужно освежить знания о шестнадцатеричной системе, то книга Чарльза Петцольда "Код: The Hidden Language - отличное место для этого. Hex - это система счисления по основанию 16, в которой вместо 0-9 используются 0-9 и a->f в качестве основных цифр.

Наконец, давайте вернемся к тому, с чего начали, с последовательности случайных байтов x. Надеюсь, теперь это имеет немного больше смысла. Вызов .hex() на объекте bytes дает str шестнадцатеричных чисел, каждое из которых соответствует десятичному числу от 0 до 255:

>>> x
b'\xce\x11\xe7"!\x84'

>>> list(x)
[206, 17, 231, 34, 33, 132]

>>> x.hex()
'ce11e7222184'

>>> len(x.hex())
12

Последний вопрос: как получилось, что длина b.hex() составляет 12 символов, хотя x - это всего 6 байт? Это потому, что две шестнадцатеричные цифры точно соответствуют одному байту. Версия str для bytes всегда будет вдвое длиннее, насколько это возможно для наших глаз.

Даже если для представления байта (например, \x01) не требуется полных 8 бит, b.hex() всегда будет использовать две шестнадцатеричные цифры на байт, поэтому число 1 будет представлено как 01, а не просто 1. Однако с математической точки зрения оба этих числа имеют одинаковый размер.

Технические подробности: В основном вы рассмотрели, как объект bytes становится объектом Python str. Еще одна техническая особенность заключается в том, как bytes, создаваемый os.urandom(), преобразуется в float в интервале [0.0, 1.0), как в криптографически защищенной версии random.random(). Если вы хотите изучить этот вопрос подробнее, этот фрагмент кода демонстрирует, как int.from_bytes() производит начальное преобразование в целое число, используя систему счисления base-256.

После этого давайте рассмотрим недавно представленный модуль secrets, который делает генерацию защищенных токенов гораздо более удобной.

Python's Best Kept secrets

Введенный в Python 3.6 в одном из самых красочных PEP, модуль secrets должен стать де-факто модулем Python для генерации криптографически безопасных случайных байтов и строк.

Вы можете посмотреть исходный код для модуля, который короток и мил - около 25 строк кода. secrets - это, по сути, обертка вокруг os.urandom(). Он экспортирует всего несколько функций для генерации случайных чисел, байтов и строк. Большинство из этих примеров должны быть достаточно понятны:

>>> n = 16

>>> # Generate secure tokens
>>> secrets.token_bytes(n)
b'A\x8cz\xe1o\xf9!;\x8b\xf2\x80pJ\x8b\xd4\xd3'
>>> secrets.token_hex(n)
'9cb190491e01230ec4239cae643f286f'  
>>> secrets.token_urlsafe(n)
'MJoi7CknFu3YN41m88SEgQ'

>>> # Secure version of `random.choice()`
>>> secrets.choice('rain')
'a'

А теперь, как насчет конкретного примера? Вы, вероятно, пользовались сервисами сокращения URL, такими как tinyurl.com или bit.ly, которые превращают громоздкий URL в нечто вроде https://bit.ly/2IcCp9u. Большинство укорачивателей не делают никакого сложного хеширования при переходе от входного URL к выходному; они просто генерируют случайную строку, проверяют, не была ли она сгенерирована ранее, и затем привязывают ее обратно к входному URL.

Предположим, что, изучив базу данных Root Zone Database, вы зарегистрировали сайт short.ly. Вот функция, которая поможет вам начать работу с сервисом:

# shortly.py

from secrets import token_urlsafe

DATABASE = {}

def shorten(url: str, nbytes: int=5) -> str:
    ext = token_urlsafe(nbytes=nbytes)
    if ext in DATABASE:
        return shorten(url, nbytes=nbytes)
    else:
        DATABASE.update({ext: url})
        return f'short.ly/{ext}

Является ли это полноценной реальной иллюстрацией? Нет. Я бы поспорил, что bit.ly делает вещи чуть более продвинутыми, чем хранение своей золотой жилы в глобальном словаре Python, который не сохраняется между сессиями.

Примечание: Если вы хотите создать собственный полноценный сократитель URL, то ознакомьтесь с Build a URL Shortener With FastAPI and Python.

Однако концептуально это примерно верно:

>>> urls = (
...     'https://realpython.com/',
...     'https://docs.python.org/3/howto/regex.html'
... )

>>> for u in urls:
...     print(shorten(u))
short.ly/p_Z4fLI
short.ly/fuxSyNY

>>> DATABASE
{'p_Z4fLI': 'https://realpython.com/',
 'fuxSyNY': 'https://docs.python.org/3/howto/regex.html'}

Держитесь: Вы можете заметить, что оба результата имеют длину 7, в то время как вы запросили 5 байт. Погодите, вы же говорили, что результат будет в два раза длиннее? Ну, в данном случае не совсем так. Здесь происходит еще одна вещь: token_urlsafe() использует кодировку base64, где каждый символ - это 6 бит данных. (Это от 0 до 63 и соответствующие символы. Символы - это A-Z, a-z, 0-9 и +/.)

Если вы изначально задали определенное количество байт nbytes, то результирующая длина secrets.token_urlsafe(nbytes) будет math.ceil(nbytes * 8 / 6), что вы можете доказать и исследовать дальше, если вам любопытно.

Суть в том, что, хотя secrets - это всего лишь обертка для существующих функций Python, она может стать вашим помощником, если безопасность стоит на первом месте.

Последний кандидат: uuid

Последним вариантом генерации случайного маркера является функция uuid4() из модуля uuid в Python. UUID - это универсальный уникальный идентификатор, 128-битная последовательность (str длины 32), разработанная для "гарантии уникальности в пространстве и времени". uuid4() - одна из самых полезных функций модуля, и эта функция также использует os.urandom():

>>> import uuid

>>> uuid.uuid4()
UUID('3e3ef28d-3ff0-4933-9bba-e5ee91ce0e7b')
>>> uuid.uuid4()
UUID('2e115fcb-5761-4fa1-8287-19f4ee2877ac')

Приятно то, что все функции uuid создают экземпляр класса UUID, который инкапсулирует идентификатор и имеет такие свойства, как .int, .bytes и .hex:

>>> tok = uuid.uuid4()
>>> tok.bytes
b'.\xb7\x80\xfd\xbfIG\xb3\xae\x1d\xe3\x97\xee\xc5\xd5\x81'

>>> len(tok.bytes)
16
>>> len(tok.bytes) * 8  # In bits
128

>>> tok.hex
'2eb780fdbf4947b3ae1de397eec5d581'
>>> tok.int
62097294383572614195530565389543396737

Возможно, вы видели и другие варианты: uuid1(), uuid3() и uuid5(). Ключевое различие между ними и uuid4() заключается в том, что все эти три функции принимают некоторую форму ввода и поэтому не соответствуют определению "случайный" в той степени, в которой это делает UUID версии 4:

  • uuid1() по умолчанию использует идентификатор хоста вашей машины и текущее время. Из-за опоры на текущее время с разрешением до наносекунды именно эта версия UUID получила утверждение "гарантированная уникальность во времени".

  • uuid3() и uuid5() принимают идентификатор пространства имен и имя. В первом случае используется хэш MD5, а во втором - SHA-1.

uuid4(), наоборот, полностью псевдослучайна (или случайна). Он состоит из получения 16 байт через os.urandom(), преобразования их в целое число big-endian и выполнения ряда побитовых операций для соответствия формальной спецификации.

Надеемся, к этому моменту вы уже имеете представление о различии между разными "типами" случайных данных и о том, как их создавать. Однако еще один вопрос, который может прийти вам на ум, - это коллизии.

В этом случае столкновение означает просто генерацию двух совпадающих UUID. Какова вероятность этого? Ну, технически он не равен нулю, но, возможно, достаточно близок: существует 2 ** 128 или 340 ундециллионов возможных uuid4 значений. Итак, я оставляю на ваше усмотрение, является ли это достаточной гарантией, чтобы спать спокойно.

Одно из распространенных применений uuid - в Django, где есть UUIDField, который часто используется как первичный ключ в реляционной базе данных, лежащей в основе модели.

Почему бы не сделать "По умолчанию" SystemRandom?

Помимо обсуждаемых здесь безопасных модулей, таких как secrets, в модуле random Python есть малоиспользуемый класс SystemRandom, который использует os.urandom(). (SystemRandom, в свою очередь, также используется secrets. Все это - паутина, восходящая к urandom().)

На данный момент вы можете спросить себя, почему бы просто не установить эту версию "по умолчанию"? Почему бы не "всегда быть в безопасности", вместо того чтобы по умолчанию использовать детерминированные random функции,

которые не являются криптографически безопасными?

Я уже упоминал одну причину: иногда вы хотите, чтобы ваши данные были детерминированными и воспроизводимыми, чтобы другие могли следовать за ними.

Но вторая причина заключается в том, что CSPRNG, по крайней мере в Python, как правило, значительно медленнее, чем PRNG. Давайте проверим это с помощью скрипта timed.py, который сравнивает ГПСЧ и ЦСПГ версии randint() с помощью Python's timeit.repeat():

# timed.py

import random
import timeit

# The "default" random is actually an instance of `random.Random()`.
# The CSPRNG version uses `SystemRandom()` and `os.urandom()` in turn.
_sysrand = random.SystemRandom()

def prng() -> None:
    random.randint(0, 95)

def csprng() -> None:
    _sysrand.randint(0, 95)

setup = 'import random; from __main__ import prng, csprng'

if __name__ == '__main__':
    print('Best of 3 trials with 1,000,000 loops per trial:')

    for f in ('prng()', 'csprng()'):
        best = min(timeit.repeat(f, setup=setup))
        print('\t{:8s} {:0.2f} seconds total time.'.format(f, best))

Теперь выполним это из оболочки:

$ python3 ./timed.py
Best of 3 trials with 1,000,000 loops per trial:
        prng()   1.07 seconds total time.
        csprng() 6.20 seconds total time.

Разница во времени в 5 раз, безусловно, является важным фактором, помимо криптографической безопасности, при выборе одного из двух вариантов.

Odds and Ends: Hashing

Одна из концепций, которой не уделялось много внимания в этом учебнике, - это хэширование, которое можно выполнить с помощью модуля hashlib в Python.

Хеш предназначен для одностороннего отображения входного значения в строку фиксированного размера, которую практически невозможно перепрограммировать. Поэтому, хотя результат работы хэш-функции может "выглядеть" как случайные данные, он не подходит под данное определение.

Recap

В этом учебнике вы проделали большую работу. Вкратце, вот сравнение доступных вам вариантов создания случайности в Python:

Package/Module Description Cryptographically Secure
random Fasty & easy random data using Mersenne Twister No
numpy.random Like random but for (possibly multidimensional) arrays No
os Contains urandom(), the base of other functions covered here Yes
secrets Designed to be Python’s de facto module for generating secure random numbers, bytes, and strings Yes
uuid Home to a handful of functions for building 128-bit identifiers Yes, uuid4()

Не стесняйтесь оставлять совершенно случайные комментарии ниже, и спасибо, что читаете.

Вернуться на верх