Программирование массивов с помощью NumPy

Оглавление

• Getting into Shape: Знакомство с массивами NumPy
• Что такое векторизация?
  • Счет: Легко как 1, 2, 3...
  • Покупай низко, продавай высоко
• Интермеццо: понимание обозначения осей
• Трансляция
• Массовое программирование в действии: Примеры
  • Алгоритмы кластеризации
  • Амортизационные таблицы
  • Извлечение характеристик изображения
• Напутственная мысль: Не переусердствуйте с оптимизацией
• Дополнительные ресурсы

Иногда говорят, что Python, по сравнению с низкоуровневыми языками, такими как C++, улучшает время разработки за счет времени выполнения. К счастью, существует несколько способов ускорить время выполнения операций в Python без ущерба для простоты использования. Одним из вариантов, подходящих для быстрых численных операций, является NumPy, который заслуженно называет себя фундаментальным пакетом для научных вычислений на Python.

Согласитесь, мало кто отнесет к категории "медленных" то, что занимает 50 микросекунд (пятьдесят миллионных долей секунды). Однако компьютеры могут с этим не согласиться. Время выполнения операции, занимающей 50 микросекунд (50 мкс), относится к области микропроизводительности, которую можно условно определить как операции со временем выполнения от 1 микросекунды до 1 миллисекунды.

Почему скорость имеет значение? Микропроизводительность стоит отслеживать потому, что небольшие различия во времени выполнения усиливаются при повторных вызовах функций: дополнительные 50 мкс накладных расходов, повторенные при 1 миллионе вызовов функций, превращаются в 50 секунд дополнительного времени выполнения.

Когда дело доходит до вычислений, есть три концепции, которые придают NumPy силу:

• Векторизация
• Бродкастинг
• Индексирование

В этом уроке вы шаг за шагом увидите, как использовать преимущества векторизации и трансляции, чтобы использовать NumPy на полную мощность. Хотя здесь вы будете использовать индексацию на практике, полная схема индексации NumPy, которая расширяет синтаксис Python slicing syntax, - это отдельный зверь. Если вы хотите прочитать больше об индексировании в NumPy, возьмите кофе и отправляйтесь в раздел Indexing в документации NumPy.

Приведение себя в форму: Знакомство с массивами NumPy

Основополагающим объектом NumPy является его ndarray (или numpy.array), n-мерный массив, который в той или иной форме присутствует в таких ориентированных на массивы языках, как Fortran 90, R и MATLAB, а также предшественниках APL и J.

Начнем с формирования 3-мерного массива из 36 элементов:

>>> import numpy as np

>>> arr = np.arange(36).reshape(3, 4, 3)
>>> arr
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8],
        [ 9, 10, 11]],

       [[12, 13, 14],
        [15, 16, 17],
        [18, 19, 20],
        [21, 22, 23]],

       [[24, 25, 26],
        [27, 28, 29],
        [30, 31, 32],
        [33, 34, 35]]])

Представление двумерных массивов в двух измерениях может быть затруднительным. Один из интуитивных способов представить форму массива - просто "прочитать его слева направо". arr - это массив 3 на 4 на 3:

>>> arr.shape
(3, 4, 3)

Визуально arr можно представить как контейнер из трех сеток 4х3 (или прямоугольную призму), и он будет выглядеть так:

Массивы большей размерности могут быть сложнее представить, но они все равно будут следовать этой схеме "массивы внутри массива".

Где вы можете увидеть данные с более чем двумя измерениями?

• Панельные данные могут быть представлены в трех измерениях. Данные, которые отслеживают атрибуты когорты (группы) людей с течением времени, могут быть структурированы как (respondents, dates, attributes). В 1979 году Национальное продольное исследование молодежи охватывало 12 686 респондентов в течение 27 лет. Если предположить, что на одного человека приходится ~500 непосредственно заданных или полученных точек данных в год, то эти данные будут иметь форму (12686, 27, 500) в общей сложности 177 604 000 точек данных.
• Данные о цветных изображениях для нескольких изображений обычно хранятся в четырех измерениях. Каждое изображение представляет собой трехмерный массив (height, width, channels), где каналами обычно являются значения красного, зеленого и синего цветов (RGB). Коллекция изображений - это просто (image_number, height, width, channels). Тысяча изображений RGB размером 256x256 будут иметь форму (1000, 256, 256, 3). (Расширенное представление - RGBA, где A-альфа обозначает уровень непрозрачности.)

Более подробно о реальных примерах высокоразмерных данных см. главу 2 книги Франсуа Шолле "Глубокое обучение с помощью Python" .

Что такое векторизация?

Векторизация - это мощная способность NumPy выражать операции над целыми массивами, а не над их отдельными элементами. Вот краткое определение от Уэса МакКинни:

Такую практику замены явных циклов выражениями массивов принято называть векторизацией. В целом, векторизованные операции с массивами часто оказываются на один или два (или более) порядка быстрее, чем их эквиваленты в чистом Python, причем наибольший эффект [наблюдается] при любых численных вычислениях. [source]

При выполнении цикла над массивом или любой структурой данных в Python возникает много накладных расходов. Векторные операции в NumPy делегируют внутреннюю обработку циклов высоко оптимизированным функциям C и Fortran, что делает код на Python чище и быстрее.

Подсчет: Легко как 1, 2, 3...

В качестве иллюстрации рассмотрим одномерный вектор из True и False, для которого нужно подсчитать количество переходов от ложного к истинному в последовательности:

>>> np.random.seed(444)

>>> x = np.random.choice([False, True], size=100000)
>>> x
array([ True, False,  True, ...,  True, False,  True])

При использовании цикла Python for одним из способов сделать это будет попарная оценка истинного значения каждого элемента в последовательности вместе с элементом, который идет сразу после него:

>>> def count_transitions(x) -> int:
...     count = 0
...     for i, j in zip(x[:-1], x[1:]):
...         if j and not i:
...             count += 1
...     return count
...
>>> count_transitions(x)
24984

В векторной форме нет явного цикла for или прямого обращения к отдельным элементам:

>>> np.count_nonzero(x[:-1] < x[1:])
24984

Как эти две эквивалентные функции соотносятся по производительности? В данном конкретном случае векторизованный вызов NumPy выигрывает примерно в 70 раз:

>>> from timeit import timeit
>>> setup = 'from __main__ import count_transitions, x; import numpy as np'
>>> num = 1000
>>> t1 = timeit('count_transitions(x)', setup=setup, number=num)
>>> t2 = timeit('np.count_nonzero(x[:-1] < x[1:])', setup=setup, number=num)
>>> print('Speed difference: {:0.1f}x'.format(t1 / t2))
Speed difference: 71.0x

Технические подробности: Другой термин - векторный процессор, относящийся к аппаратному обеспечению компьютера. Говоря здесь о векторизации, я имею в виду концепцию замены явных for циклов выражениями массивов, которые в этом случае могут быть вычислены внутренними средствами низкоуровневого языка.

Покупайте низко, продавайте высоко

Вот еще один пример, чтобы разжечь ваш аппетит. Рассмотрим следующую классическую проблему технического интервью:

Учитывая историю цен акции в виде последовательности и предполагая, что вам разрешено совершить только одну покупку и одну продажу, какую максимальную прибыль можно получить? Например, при prices = (20, 18, 14, 17, 20, 21, 15) максимальная прибыль составит 7 от покупки по цене 14 и продажи по цене 21.

(Для всех вас, финансистов: нет, короткие продажи не разрешены)

Существует решение с n-квадратичной временной сложностью, которое состоит в том, чтобы взять каждую комбинацию двух цен, где вторая цена "идет после" первой, и определить максимальную разницу.

Однако существует и O(n) решение, которое состоит в том, чтобы пройтись по последовательности всего один раз и найти разницу между каждой ценой и бегущим минимумом. Это выглядит примерно так:

>>> def profit(prices):
...     max_px = 0
...     min_px = prices[0]
...     for px in prices[1:]:
...         min_px = min(min_px, px)
...         max_px = max(px - min_px, max_px)
...     return max_px

>>> prices = (20, 18, 14, 17, 20, 21, 15)
>>> profit(prices)
7

Можно ли это сделать в NumPy? Конечно. Но сначала давайте построим квазиреалистичный пример:

# Create mostly NaN array with a few 'turning points' (local min/max).
>>> prices = np.full(100, fill_value=np.nan)
>>> prices[[0, 25, 60, -1]] = [80., 30., 75., 50.]

# Linearly interpolate the missing values and add some noise.
>>> x = np.arange(len(prices))
>>> is_valid = ~np.isnan(prices)
>>> prices = np.interp(x=x, xp=x[is_valid], fp=prices[is_valid])
>>> prices += np.random.randn(len(prices)) * 2

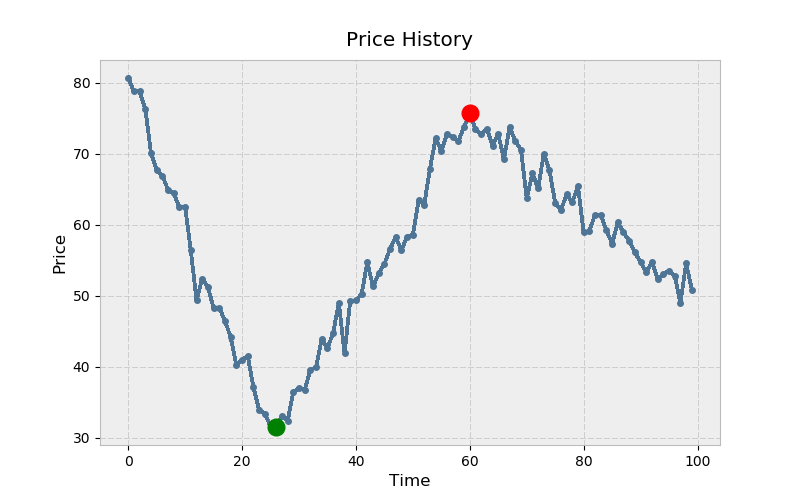
Вот как это выглядит с помощью matplotlib. Поговорка гласит: покупай низко (зеленый) и продавай высоко (красный):

>>> import matplotlib.pyplot as plt

# Warning! This isn't a fully correct solution, but it works for now.
# If the absolute min came after the absolute max, you'd have trouble.
>>> mn = np.argmin(prices)
>>> mx = mn + np.argmax(prices[mn:])
>>> kwargs = {'markersize': 12, 'linestyle': ''}

>>> fig, ax = plt.subplots()
>>> ax.plot(prices)
>>> ax.set_title('Price History')
>>> ax.set_xlabel('Time')
>>> ax.set_ylabel('Price')
>>> ax.plot(mn, prices[mn], color='green', **kwargs)
>>> ax.plot(mx, prices[mx], color='red', **kwargs)

Как выглядит реализация NumPy? Хотя нет np.cummin() "напрямую", у универсальных функций (ufuncs) NumPy есть accumulate() метод, который делает то, что следует из его названия:

>>> cummin = np.minimum.accumulate

Расширяя логику из чистого примера на Python, вы можете найти разницу между каждой ценой и текущим минимумом (по элементам), а затем взять максимум из этой последовательности:

>>> def profit_with_numpy(prices):
...     """Price minus cumulative minimum price, element-wise."""
...     prices = np.asarray(prices)
...     return np.max(prices - cummin(prices))

>>> profit_with_numpy(prices)
44.2487532293278
>>> np.allclose(profit_with_numpy(prices), profit(prices))
True

Как эти две операции, имеющие одинаковую теоретическую временную сложность, соотносятся в реальном времени выполнения? Сначала возьмем более длинную последовательность. (На данный момент это не обязательно должен быть временной ряд цен на акции.)

>>> seq = np.random.randint(0, 100, size=100000)
>>> seq
array([ 3, 23,  8, 67, 52, 12, 54, 72, 41, 10, ..., 46,  8, 90, 95, 93,
       28, 24, 88, 24, 49])

Теперь, для несколько несправедливого сравнения:

>>> setup = ('from __main__ import profit_with_numpy, profit, seq;'
...          ' import numpy as np')
>>> num = 250
>>> pytime = timeit('profit(seq)', setup=setup, number=num)
>>> nptime = timeit('profit_with_numpy(seq)', setup=setup, number=num)
>>> print('Speed difference: {:0.1f}x'.format(pytime / nptime))
Speed difference: 76.0x

Выше, рассматривая profit_with_numpy() как псевдокод (без учета базовой механики NumPy), фактически существует три прохода через последовательность:

• cummin(prices) имеет временную сложность O(n)
• prices - cummin(prices) имеет O(n)
• max(...) имеет сложность O(n)

Это сводится к O(n), потому что O(3n) сводится к просто O(n)- n "доминирует" по мере приближения n к бесконечности.

Следовательно, эти две функции имеют эквивалентную наихудшую временную сложность. (Хотя, как примечание, функция NumPy имеет значительно большую пространственную сложность). Но это, пожалуй, наименее важный вывод. Один из уроков заключается в том, что, хотя теоретическая временная сложность является важным соображением, механика времени выполнения также может играть большую роль. NumPy не только может делегировать полномочия на C, но и, используя некоторые операции с мудрыми элементами и линейную алгебру, может использовать преимущества вычислений в нескольких потоках. Но здесь играет роль множество факторов, включая используемую базовую библиотеку (BLAS/LAPACK/Atlas), и эти детали - для совсем другой статьи.

Интермеццо: Понимание обозначения осей

В NumPy ось относится к одному измерению многомерного массива:

>>> arr = np.array([[1, 2, 3],
...                 [10, 20, 30]])
>>> arr.sum(axis=0)
array([11, 22, 33])
>>> arr.sum(axis=1)
array([ 6, 60])

Терминология, связанная с осями, и способ их описания могут быть немного неинтуитивными. В документации к Pandas (библиотеке, построенной поверх NumPy) часто можно встретить что-то вроде:

axis : {'index' (0), 'columns' (1)}

Можно утверждать, что, исходя из этого описания, приведенные выше результаты должны быть "перевернуты". Однако ключевым моментом является то, что axis относится к оси , вдоль которой вызывается функция. Это хорошо сформулировал Джейк Вандерплас:

То, как здесь задается ось, может сбить с толку пользователей, пришедших из других языков. Ключевое слово axis указывает размерность массива, который будет свернут, а не размерность, которая будет возвращена. Так, указание axis=0 означает, что будет свернута первая ось: для двумерных массивов это означает, что значения в каждом столбце будут агрегированы. [source]

Другими словами, суммирование массива за axis=0 сворачивает строки массива с вычислением по столбцам.

Помня об этом различии, давайте перейдем к изучению концепции вещания.

Бродкастинг

Бродкастинг - еще одна важная абстракция NumPy. Вы уже видели, что операции между двумя массивами NumPy (одинакового размера) работают элементно:

>>> a = np.array([1.5, 2.5, 3.5])
>>> b = np.array([10., 5., 1.])
>>> a / b
array([0.15, 0.5 , 3.5 ])

Но как быть с массивами неравного размера? Здесь на помощь приходит трансляция:

Термин трансляция описывает, как NumPy обращается с массивами разной формы во время арифметических операций. При соблюдении определенных ограничений меньший массив "транслируется" на больший массив, чтобы они имели совместимые формы. Трансляция предоставляет возможность векторизации операций с массивами, так что зацикливание происходит на C, а не на Python. [source]

Способ, которым реализована трансляция, может стать утомительным при работе с более чем двумя массивами. Однако если массивов всего два, то их способность к трансляции можно описать двумя короткими правилами:

При работе с двумя массивами NumPy сравнивает их формы по элементам. Он начинает с следящих размеров и работает дальше. Два измерения совместимы, если:

1. они равны, или
2. одно из них равно 1

Вот и все.

Давайте рассмотрим случай, когда мы хотим вычесть из массива среднее значение по каждому столбцу поэлементно:

>>> sample = np.random.normal(loc=[2., 20.], scale=[1., 3.5],
...                           size=(3, 2))
>>> sample
array([[ 1.816 , 23.703 ],
       [ 2.8395, 12.2607],
       [ 3.5901, 24.2115]])

<<<На статистическом жаргоне

sample состоит из двух выборок (столбцов), взятых независимо из двух популяций со средними значениями 2 и 20 соответственно. Средние по столбцам должны приближаться к средним по популяции (хотя и приблизительно, поскольку выборка мала):

>>> mu = sample.mean(axis=0)
>>> mu
array([ 2.7486, 20.0584])

Теперь вычитание средних по столбцам не вызывает затруднений, поскольку правила трансляции выполняются:

>>> print('sample:', sample.shape, '| means:', mu.shape)
sample: (3, 2) | means: (2,)

>>> sample - mu
array([[-0.9325,  3.6446],
       [ 0.091 , -7.7977],
       [ 0.8416,  4.1531]])

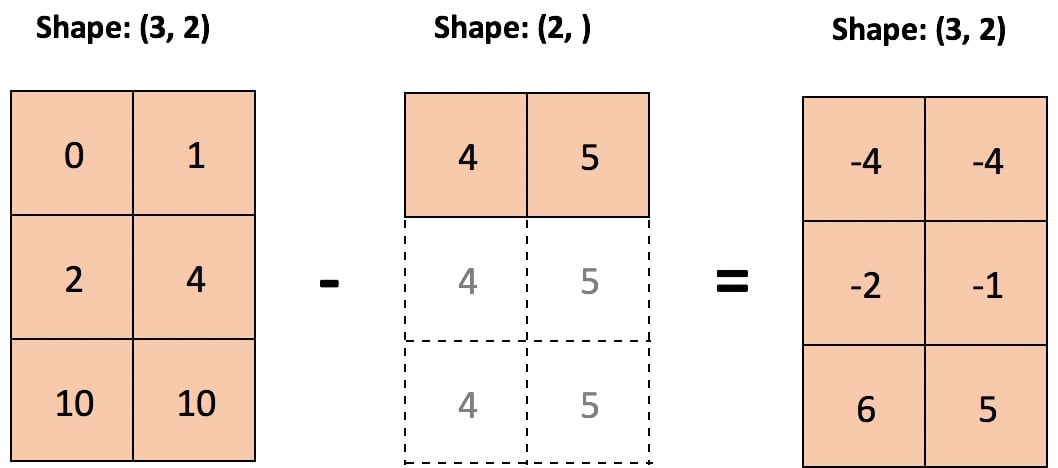
Вот иллюстрация вычитания по столбцам, когда меньший массив "растягивается" так, что он вычитается из каждой строки большего массива:

Техническая деталь: Массив или скаляр меньшего размера не растягивается в памяти буквально: повторяется само вычисление.

Это распространяется и на стандартизацию каждого столбца, делая каждую ячейку z-score относительно соответствующего столбца:

>>> (sample - sample.mean(axis=0)) / sample.std(axis=0)
array([[-1.2825,  0.6605],
       [ 0.1251, -1.4132],
       [ 1.1574,  0.7527]])

Однако что, если вы хотите вычесть по какой-то причине минимальные значения в ряду? Вы столкнетесь с небольшими проблемами:

>>> sample - sample.min(axis=1)
ValueError: operands could not be broadcast together with shapes (3,2) (3,)

Проблема здесь в том, что меньший массив в его текущей форме не может быть "растянут", чтобы стать совместимым по форме с sample. На самом деле вам нужно увеличить его размерность, чтобы удовлетворить правилам трансляции, приведенным выше:

>>> sample.min(axis=1)[:, None]  # 3 minimums across 3 rows
array([[1.816 ],
       [2.8395],
       [3.5901]])

>>> sample - sample.min(axis=1)[:, None]
array([[ 0.    , 21.887 ],
       [ 0.    ,  9.4212],
       [ 0.    , 20.6214]])

Примечание: [:, None] - это средство для расширения размерности массива, чтобы создать ось длины один. np.newaxis является псевдонимом для None.

Есть и значительно более сложные случаи. Вот более строгое определение того, когда произвольное количество массивов любой формы NumPy может быть передано вместе:

Набор массивов называется "транслируемым" в одну и ту же форму NumPy, если следующие правила дают корректный результат, то есть одно из следующих верно:

1. Все массивы имеют одинаковую форму.

2. Все массивы имеют одинаковое количество измерений, и длина каждого измерения равна либо общей длине, либо 1.

3. К массивам, имеющим слишком мало измерений, формы NumPy могут добавлять измерение длины 1, чтобы удовлетворить свойству #2.

[source]

Так легче пройти шаг за шагом. Допустим, у вас есть следующие четыре массива:

>>> a = np.sin(np.arange(10)[:, None])
>>> b = np.random.randn(1, 10)
>>> c = np.full_like(a, 10)
>>> d = 8

Перед проверкой форм NumPy сначала преобразует скаляры в массивы с одним элементом:

>>> arrays = [np.atleast_1d(arr) for arr in (a, b, c, d)]
>>> for arr in arrays:
...     print(arr.shape)
...
(10, 1)
(1, 10)
(10, 1)
(1,)

Теперь мы можем проверить критерий №1. Если все массивы имеют одинаковую форму, то set их формы сгустятся до одного элемента, потому что конструктор set() эффективно удаляет дубликаты со своего входа. Этот критерий явно не выполняется:

>>> len(set(arr.shape for arr in arrays)) == 1
False

Первая часть критерия №2 также не работает, а значит, не работает и весь критерий:

>>> len(set((arr.ndim) for arr in arrays)) == 1
False

Последний критерий немного сложнее:

К массивам, имеющим слишком мало измерений, можно добавить размерность длиной 1, чтобы удовлетворить свойство #2.

Для кодирования этого можно сначала определить размерность массива наибольшей размерности, а затем добавлять единицы к каждому кортежу NumPy shape, пока все они не станут одинаковой размерности:

>>> maxdim = max(arr.ndim for arr in arrays)  # Maximum dimensionality
>>> shapes = np.array([(1,) * (maxdim - arr.ndim) + arr.shape
...                    for arr in arrays])
>>> shapes
array([[10,  1],
       [ 1, 10],
       [10,  1],
       [ 1,  1]])

Наконец, необходимо проверить, что длина каждого измерения либо равна (взята из) общей длины, либо равна 1. Для этого нужно сначала замаскировать массив NumPy "shape-tuples" в тех местах, где он равен единице. Затем можно проверить, все ли разности между столбцами равны нулю:

>>> masked = np.ma.masked_where(shapes == 1, shapes)
>>> np.all(masked.ptp(axis=0) == 0)  # ptp: max - min
True

Выраженная в одной функции, эта логика выглядит следующим образом:

>>> def can_broadcast(*arrays) -> bool:
...     arrays = [np.atleast_1d(arr) for arr in arrays]
...     if len(set(arr.shape for arr in arrays)) == 1:
...         return True
...     if len(set((arr.ndim) for arr in arrays)) == 1:
...         return True
...     maxdim = max(arr.ndim for arr in arrays)
...     shapes = np.array([(1,) * (maxdim - arr.ndim) + arr.shape
...                        for arr in arrays])
...     masked = np.ma.masked_where(shapes == 1, shapes)
...     return np.all(masked.ptp(axis=0) == 0)
...
>>> can_broadcast(a, b, c, d)
True

К счастью, вы можете сократить путь и использовать np.broadcast() для этой проверки на вменяемость, хотя он и не предназначен для этого:

>>> def can_broadcast(*arrays) -> bool:
...     try:
...         np.broadcast(*arrays)
...         return True
...     except ValueError:
...         return False
...
>>> can_broadcast(a, b, c, d)
True

Для тех, кто хочет копнуть немного глубже, PyArray_Broadcast - это базовая функция на языке C, которая инкапсулирует правила вещания.

Массивное программирование в действии: Примеры

В следующих 3 примерах вы примените векторизацию и трансляцию в некоторых реальных приложениях.

Алгоритмы кластеризации

Машинное обучение - одна из областей, в которой часто можно использовать преимущества векторизации и трансляции. Допустим, у вас есть вершины треугольника (каждая строка - это координаты x, y):

>>> tri = np.array([[1, 1],
...                 [3, 1],
...                 [2, 3]])

центроид этого "кластера" - это координата (x, y), которая является средним арифметическим каждого столбца:

>>> centroid = tri.mean(axis=0)
>>> centroid
array([2.    , 1.6667])

Полезно представить себе это так:

>>> trishape = plt.Polygon(tri, edgecolor='r', alpha=0.2, lw=5)
>>> _, ax = plt.subplots(figsize=(4, 4))
>>> ax.add_patch(trishape)
>>> ax.set_ylim([.5, 3.5])
>>> ax.set_xlim([.5, 3.5])
>>> ax.scatter(*centroid, color='g', marker='D', s=70)
>>> ax.scatter(*tri.T, color='b',  s=70)

Многие алгоритмы кластеризации используют евклидовы расстояния между множеством точек, либо до начала координат, либо относительно их центроидов.

В декартовых координатах евклидово расстояние между точками p и q равно:

[источник: Википедия]

Так, для набора координат в tri сверху, евклидово расстояние каждой точки от начала координат (0, 0) будет:

>>> np.sum(tri**2, axis=1) ** 0.5  # Or: np.sqrt(np.sum(np.square(tri), 1))
array([1.4142, 3.1623, 3.6056])

Вы можете понять, что на самом деле мы просто находим евклидовы нормы:

>>> np.linalg.norm(tri, axis=1)
array([1.4142, 3.1623, 3.6056])

Вместо того чтобы ссылаться на начало координат, можно также найти нормаль каждой точки относительно центроида треугольника:

>>> np.linalg.norm(tri - centroid, axis=1)
array([1.2019, 1.2019, 1.3333])

Наконец, давайте сделаем еще один шаг вперед: допустим, у вас есть двумерный массив X и двумерный массив из множества (x, y) "предложенных" центроидов. Такие алгоритмы, как кластеризация K-Means, работают путем случайного назначения начальных "предполагаемых" центроидов, а затем переназначения каждой точки данных на ближайший к ней центроид. После этого вычисляются новые центроиды, причем алгоритм сходится к решению, когда сгенерированные метки (кодировка центроидов) остаются неизменными между итерациями. Часть этого итерационного процесса требует вычисления евклидова расстояния каждой точки от каждого центроида:

>>> X = np.repeat([[5, 5], [10, 10]], [5, 5], axis=0)
>>> X = X + np.random.randn(*X.shape)  # 2 distinct "blobs"
>>> centroids = np.array([[5, 5], [10, 10]])

>>> X
array([[ 3.3955,  3.682 ],
       [ 5.9224,  5.785 ],
       [ 5.9087,  4.5986],
       [ 6.5796,  3.8713],
       [ 3.8488,  6.7029],
       [10.1698,  9.2887],
       [10.1789,  9.8801],
       [ 7.8885,  8.7014],
       [ 8.6206,  8.2016],
       [ 8.851 , 10.0091]])

>>> centroids
array([[ 5,  5],
       [10, 10]])

Другими словами, мы хотим ответить на вопрос, к какому центроиду принадлежит каждая точка в пределах X? Здесь нам необходимо выполнить некоторую перестройку, чтобы вычислить евклидово расстояние между каждой точкой в X и каждой точкой в centroids:

>>> centroids[:, None]
array([[[ 5,  5]],

       [[10, 10]]])

>>> centroids[:, None].shape
(2, 1, 2)

Это позволяет нам чисто вычитать один массив из другого, используя комбинаторное произведение их строк:

>>> np.linalg.norm(X - centroids[:, None], axis=2).round(2)
array([[2.08, 1.21, 0.99, 1.94, 2.06, 6.72, 7.12, 4.7 , 4.83, 6.32],
       [9.14, 5.86, 6.78, 7.02, 6.98, 0.73, 0.22, 2.48, 2.27, 1.15]])

Другими словами, форма NumPy для X - centroids[:, None] равна (2, 10, 2), по сути представляя собой два сложенных массива, каждый из которых имеет размер X. Далее нам нужна метка (номер индекса) каждого ближайшего центроида, находящего минимальное расстояние по оси 0 от массива выше:

>>> np.argmin(np.linalg.norm(X - centroids[:, None], axis=2), axis=0)
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])

Вы можете представить все это в функциональной форме:

>>> def get_labels(X, centroids) -> np.ndarray:
...     return np.argmin(np.linalg.norm(X - centroids[:, None], axis=2),
...                      axis=0)
>>> labels = get_labels(X, centroids)

Давайте проверим это визуально, изобразив два кластера и присвоенные им метки с помощью цветового отображения:

>>> c1, c2 = ['#bc13fe', '#be0119']  # https://xkcd.com/color/rgb/
>>> llim, ulim  = np.trunc([X.min() * 0.9, X.max() * 1.1])

>>> _, ax = plt.subplots(figsize=(5, 5))
>>> ax.scatter(*X.T, c=np.where(labels, c2, c1), alpha=0.4, s=80)
>>> ax.scatter(*centroids.T, c=[c1, c2], marker='s', s=95,
...            edgecolor='yellow')
>>> ax.set_ylim([llim, ulim])
>>> ax.set_xlim([llim, ulim])
>>> ax.set_title('One K-Means Iteration: Predicted Classes')

Таблицы амортизации

Векторизация находит применение и в финансах.

Учитывая годовую процентную ставку, частоту платежей (раз в год), начальный остаток по кредиту и срок кредитования, можно создать амортизационную таблицу с ежемесячными остатками по кредиту и платежами в векторном виде. Сначала зададим некоторые скалярные константы:

>>> freq = 12     # 12 months per year
>>> rate = .0675  # 6.75% annualized
>>> nper = 30     # 30 years
>>> pv = 200000   # Loan face value

>>> rate /= freq  # Monthly basis
>>> nper *= freq  # 360 months

NumPy поставляется с горсткой финансовых функций, которые, в отличие от своих кузенов из Excel, способны создавать векторные выходные данные.

Должник (или арендатор) ежемесячно выплачивает постоянную сумму, состоящую из основного долга и процентной составляющей. По мере уменьшения остатка задолженности по кредиту процентная часть общего платежа уменьшается.

>>> periods = np.arange(1, nper + 1, dtype=int)
>>> principal = np.ppmt(rate, periods, nper, pv)
>>> interest = np.ipmt(rate, periods, nper, pv)
>>> pmt = principal + interest  # Or: pmt = np.pmt(rate, nper, pv)

Далее вам нужно рассчитать ежемесячный баланс, как до, так и после платежа за месяц, который можно определить как будущую стоимость первоначального баланса минус будущая стоимость аннуитета (потока платежей), используя коэффициент дисконтирования d:

Функционально это выглядит так:

>>> def balance(pv, rate, nper, pmt) -> np.ndarray:
...     d = (1 + rate) ** nper  # Discount factor
...     return pv * d - pmt * (d - 1) / rate

Наконец, вы можете перевести это в табличный формат с помощью Pandas DataFrame. Будьте осторожны со знаками. PMT - это отток с точки зрения должника.

>>> import pandas as pd

>>> cols = ['beg_bal', 'prin', 'interest', 'end_bal']
>>> data = [balance(pv, rate, periods - 1, -pmt),
...         principal,
...         interest,
...         balance(pv, rate, periods, -pmt)]

>>> table = pd.DataFrame(data, columns=periods, index=cols).T
>>> table.index.name = 'month'

>>> with pd.option_context('display.max_rows', 6):
...     # Note: Using floats for $$ in production-level code = bad
...     print(table.round(2))
...
         beg_bal     prin  interest    end_bal
month
1      200000.00  -172.20  -1125.00  199827.80
2      199827.80  -173.16  -1124.03  199654.64
3      199654.64  -174.14  -1123.06  199480.50
...          ...      ...       ...        ...
358      3848.22 -1275.55    -21.65    2572.67
359      2572.67 -1282.72    -14.47    1289.94
360      1289.94 -1289.94     -7.26      -0.00

В конце 30-го года кредит погашен:

>>> final_month = periods[-1]
>>> np.allclose(table.loc[final_month, 'end_bal'], 0)
True

Примечание: Хотя использование плавающих элементов для представления денег может быть полезным для иллюстрации концепции в среде сценариев, использование плавающих элементов Python для финансовых расчетов в производственной среде может привести к тому, что ваши расчеты в некоторых случаях будут на копейку или две меньше.

Извлечение характеристик изображения

В последнем примере мы будем работать с изображением октября 1941 года корабля USS Lexington (CV-2), обломки которого были обнаружены у берегов Австралии в марте 2018 года. Сначала мы можем отобразить изображение в массив NumPy, состоящий из значений пикселей:

>>> from skimage import io

>>> url = ('https://www.history.navy.mil/bin/imageDownload?image=/'
...        'content/dam/nhhc/our-collections/photography/images/'
...        '80-G-410000/80-G-416362&rendition=cq5dam.thumbnail.319.319.png')
>>> img = io.imread(url, as_grey=True)

>>> fig, ax = plt.subplots()
>>> ax.imshow(img, cmap='gray')
>>> ax.grid(False)

Для простоты изображение загружается в градациях серого, в результате чего получается двумерный массив 64-битных плавающих точек, а не трехмерный массив RGBA MxNx4, причем меньшие значения обозначают более темные места:

>>> img.shape
(254, 319)

>>> img.min(), img.max()
(0.027450980392156862, 1.0)

>>> img[0, :10]  # First ten cells of the first row
array([0.8078, 0.7961, 0.7804, 0.7882, 0.7961, 0.8078, 0.8039, 0.7922,
       0.7961, 0.7961])
>>> img[-1, -10:]  # Last ten cells of the last row
array([0.0784, 0.0784, 0.0706, 0.0706, 0.0745, 0.0706, 0.0745, 0.0784,
       0.0784, 0.0824])

Одним из методов, обычно используемых в качестве промежуточного шага при анализе изображений, является выделение фрагментов. Как следует из названия, она заключается в извлечении небольших перекрывающихся подмассивов из большого массива и может использоваться в случаях, когда выгодно "обесцветить" или размыть изображение.

Эта концепция распространяется и на другие области. Например, вы будете делать нечто подобное, беря "скользящие" окна временного ряда с несколькими характеристиками (переменными). Это даже полезно для построения "Игры жизни" Конвея. (Хотя конволюция с ядром 3x3 - более прямой подход.)

Здесь мы найдем среднее значение каждого перекрывающегося участка 10x10 в пределах img. Если взять миниатюрный пример, то первый массив патчей 3x3 в левом верхнем углу img будет выглядеть так:

>>> img[:3, :3]
array([[0.8078, 0.7961, 0.7804],
       [0.8039, 0.8157, 0.8078],
       [0.7882, 0.8   , 0.7961]])

>>> img[:3, :3].mean()
0.7995642701525054

Чисто питоновский подход к созданию скользящих патчей включает в себя вложенный цикл for. При этом необходимо учитывать, что начальный индекс крайних правых патчей будет находиться в индексе n - 3 + 1, где n - ширина массива. Другими словами, если бы вы извлекали патчи 3x3 из массива 10x10 под названием arr, то последний взятый патч был бы из arr[7:10, 7:10]. Также следует помнить, что в Python range() не включает параметр stop:

>>> size = 10
>>> m, n = img.shape
>>> mm, nn = m - size + 1, n - size + 1
>>>
>>> patch_means = np.empty((mm, nn))
>>> for i in range(mm):
...     for j in range(nn):
...         patch_means[i, j] = img[i: i+size, j: j+size].mean()

>>> fig, ax = plt.subplots()
>>> ax.imshow(patch_means, cmap='gray')
>>> ax.grid(False)

В этом цикле вы выполняете множество вызовов Python.

Альтернативой, которая может быть масштабирована для больших RGB или RGBA изображений, является stride_tricks от NumPy.

Для начала полезно представить, как, учитывая размер пятна и форму изображения, будет выглядеть массив пятен более высокой размерности. У нас есть двумерный массив img с формой (254, 319) и двумерный патч (10, 10). Это означает, что наша выходная форма (перед тем как взять среднее значение каждого "внутреннего" массива 10x10) будет иметь вид:

>>> shape = (img.shape[0] - size + 1, img.shape[1] - size + 1, size, size)
>>> shape
(245, 310, 10, 10)

Вам также необходимо указать страды нового массива. Страйды массива - это кортеж байтов для перехода в каждом измерении при перемещении по массиву. Каждый пиксель в img представляет собой 64-битный (8-байтовый) float, то есть общий размер изображения составляет 254 x 319 x 8 = 648 208 байт.

>>> img.dtype
dtype('float64')

>>> img.nbytes
648208

Внутри img хранится в памяти как один непрерывный блок размером 648 208 байт. strides - это своего рода "метаданные", которые сообщают нам, на сколько байт нам нужно перескочить вперед, чтобы перейти к следующей позиции вдоль каждой оси. Мы перемещаемся по строкам блоками по 8 байт, но для перехода "вниз" от одной строки к другой нам нужно 8 x 319 = 2 552 байта.

>>> img.strides
(2552, 8)

В нашем случае строки результирующего патча будут просто повторять строки img дважды:

>>> strides = 2 * img.strides
>>> strides
(2552, 8, 2552, 8)

Теперь давайте соберем эти части вместе с помощью NumPy stride_tricks:

>>> from numpy.lib import stride_tricks

>>> patches = stride_tricks.as_strided(img, shape=shape, strides=strides)
>>> patches.shape
(245, 310, 10, 10)

Вот первый 10x10 патч:

>>> patches[0, 0].round(2)
array([[0.81, 0.8 , 0.78, 0.79, 0.8 , 0.81, 0.8 , 0.79, 0.8 , 0.8 ],
       [0.8 , 0.82, 0.81, 0.79, 0.79, 0.79, 0.78, 0.81, 0.81, 0.8 ],
       [0.79, 0.8 , 0.8 , 0.79, 0.8 , 0.8 , 0.82, 0.83, 0.79, 0.81],
       [0.8 , 0.79, 0.81, 0.81, 0.8 , 0.8 , 0.78, 0.76, 0.8 , 0.79],
       [0.78, 0.8 , 0.8 , 0.78, 0.8 , 0.79, 0.78, 0.78, 0.79, 0.79],
       [0.8 , 0.8 , 0.78, 0.78, 0.78, 0.8 , 0.8 , 0.8 , 0.81, 0.79],
       [0.78, 0.77, 0.78, 0.76, 0.77, 0.8 , 0.8 , 0.77, 0.8 , 0.8 ],
       [0.79, 0.76, 0.77, 0.78, 0.77, 0.77, 0.79, 0.78, 0.77, 0.76],
       [0.78, 0.75, 0.76, 0.76, 0.73, 0.75, 0.78, 0.76, 0.77, 0.77],
       [0.78, 0.79, 0.78, 0.78, 0.78, 0.78, 0.77, 0.76, 0.77, 0.77]])

Последний шаг очень сложный. Чтобы получить векторизованное среднее значение каждого внутреннего массива 10x10, нам нужно хорошо подумать о размерности того, что мы имеем сейчас. В результате последние два измерения должны уменьшиться, так что у нас останется один массив 245x310.

Одним из (неоптимальных) способов было бы reshape patches сначала сплющить внутренние 2d-массивы до векторов длины 100, а затем вычислить среднее по последней оси:

>>> veclen = size ** 2
>>> patches.reshape(*patches.shape[:2], veclen).mean(axis=-1).shape
(245, 310)

Однако вы также можете задать axis в виде кортежа, вычисляя среднее значение по двум последним осям, что должно быть эффективнее, чем перестроение:

>>> patches.mean(axis=(-1, -2)).shape
(245, 310)

Давайте убедимся, что все получилось, сравнив равенство с нашей зацикленной версией. Это так:

>>> strided_means = patches.mean(axis=(-1, -2))
>>> np.allclose(patch_means, strided_means)
True

Если концепция страйдов вызывает у вас слюнки, не волнуйтесь: Scikit-Learn уже встроил весь этот процесс в свой feature_extraction модуль.

Прощальная мысль: Не переоценивайте

В этой статье мы обсудили оптимизацию времени выполнения за счет использования преимуществ программирования массивов в NumPy. Когда вы работаете с большими массивами данных, важно помнить о микропроизводительности.

Однако существует подмножество случаев, когда обойтись без нативного цикла Python for не представляется возможным. Как говорил Дональд Кнут , "преждевременная оптимизация - корень всех зол". Программисты могут неверно предсказать, где в их коде появится узкое место, и потратить часы на попытку полностью векторизовать операцию, которая приведет к относительно незначительному улучшению времени выполнения.

Нет ничего плохого в том, что петли for встречаются то тут, то там. Часто бывает более продуктивно подумать об оптимизации потока и структуры всего сценария на более высоком уровне абстракции.

Дополнительные ресурсы

Бесплатный бонус: Нажмите здесь, чтобы получить доступ к бесплатному руководству по ресурсам NumPy, которое поможет вам найти лучшие учебники, видео и книги для улучшения навыков работы с NumPy.

Документация NumPy:

• Что такое NumPy?
• Бродкастинг
• Универсальные функции
• NumPy для пользователей MATLAB
• Полный справочник по NumPy индекс

Книги:

• Travis Oliphant's Guide to NumPy, 2nd ed. (Трэвис - основной создатель NumPy)
• Глава 2 ("Введение в NumPy") книги Джейка Вандерпласа Python Data Science Handbook
• Глава 4 ("Основы NumPy") и Глава 12 ("Расширенный NumPy") книги Уэса Маккинни Python for Data Analysis 2nd ed.
• Глава 2 ("The Mathematical Building Blocks of Neural Networks") из книги Франсуа Шолле Deep Learning with Python
• Роберт Йоханссон Numerical Python
• Иван Идрис: Numpy Beginner's Guide, 3rd ed.

Другие ресурсы:

• Википедия: Программирование массивов
• Конспект лекций по SciPy: Basic и Advanced NumPy
• EricsBroadcastingDoc: Array Broadcasting in NumPy
• SciPy Cookbook: Виды против копий в NumPy
• Николя Ружье: From Python to Numpy и 100 упражнений по NumPy
• Документация по TensorFlow: Семантика трансляции
• Theano docs: Broadcasting
• Эли Бендерски: Бродкастинг массивов в Numpy

Вернуться на верх